Deep Neural Network from Scratch in Rust 🦀- Part 4- Loss Function and Back Propagation

24 May 2023

---

---

After [[3. Deep Neural Network from Scratch in Rust - Part 3- Forward Propagation | Forward Propagation]] we need to define a loss function to calculate how wrong our model is at this moment. For a simple binary classification problem, the loss function is given as below.

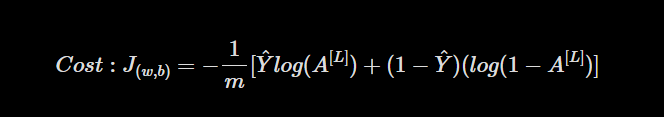
where,

m ⇾ number of training examples

Y ⇾ True Training Labels

A^L ⇾ Predicted Labels from forward propagation

The purpose of the loss function is to measure the discrepancy between the predicted labels and the true labels. By minimizing this loss, we aim to make our model’s predictions as close as possible to the ground truth.

To train the model and minimize the loss, we employ a technique called backward propagation. This technique calculates the gradients of the cost function with respect to the weights and biases, which indicates the direction and magnitude of adjustments required for each parameter. The gradient computations are performed using the following equations for each layer:

Once we have calculated the gradients, we can adjust the weights and biases to minimize the loss. The following equations are used for updating the parameters using a learning rate alpha:

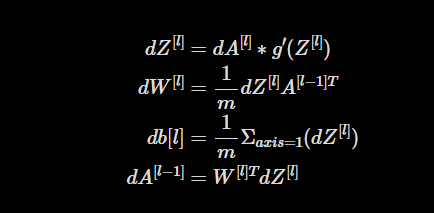
Derivations of these equations can be found here

These equations update the weights and biases of each layer based on their respective gradients. By iteratively performing the forward and backward passes, and updating the parameters using the gradients, we allow the model to learn and improve its performance over time.

---

The git repository for all the code until this part is provided in the link below. Please refer to it in case you are stuck somewhere.

Cost Function

To calculate the cost function based on the above cost equation, we need to first provide a log trait to Array2<f32> as you cannot directly take log of an array in rust. We will do this by writing the following code in the start of lib.rs

trait Log {
    fn log(&self) -> Array2<f32>;
}

impl Log for Array2<f32> {
    fn log(&self) -> Array2<f32> {
        self.mapv(|x| x.log(std::f32::consts::E))
    }
}

Next, in our impl DeepNeuralNetwork we will add a function to calculate the cost.

       pub fn cost(&self, al: &Array2<f32>, y: &Array2<f32>) -> f32 {
        let m = y.shape()[1] as f32;
        let cost = -(1.0 / m)
            * (y.dot(&al.clone().reversed_axes().log())
                + (1.0 - y).dot(&(1.0 - al).reversed_axes().log()));

        return cost.sum();
    }

Here we pass in the last layer activations al and the true labels y to calculate the cost.

---

Backward Activations

pub fn sigmoid_prime(z: &f32) -> f32 {
    sigmoid(z) * (1.0 - sigmoid(z))
}

pub fn relu_prime(z: &f32) -> f32 {
    match *z > 0.0 {
        true => 1.0,
        false => 0.0,
    }
}

pub fn sigmoid_backward(da: &Array2<f32>, activation_cache: ActivationCache) -> Array2<f32> {
    da * activation_cache.z.mapv(|x| sigmoid_prime(&x))
}

pub fn relu_backward(da: &Array2<f32>, activation_cache: ActivationCache) -> Array2<f32> {
    da * activation_cache.z.mapv(|x| relu_prime(&x))
}

The sigmoid_prime function calculates the derivative of the sigmoid activation function. It takes the input z and returns the derivative value, which is computed as the sigmoid of z multiplied by 1.0 minus the sigmoid of z.

The relu_prime function computes the derivative of the ReLU activation function. It takes the input z and returns 1.0 if z is greater than 0, and 0.0 otherwise.

The sigmoid_backward function calculates the backward propagation for the sigmoid activation function. It takes the derivative of the cost function with respect to the activation da and the activation cache activation_cache. It performs an element-wise multiplication between da and the derivative of the sigmoid function applied to the values in the activation cache, activation_cache.z.

The relu_backward function computes the backward propagation for the ReLU activation function. It takes the derivative of the cost function with respect to the activation da and the activation cache activation_cache. It performs an element-wise multiplication between da and the derivative of the ReLU function applied to the values in the activation cache, activation_cache.z.

---

Linear Backward

pub fn linear_backward(
    dz: &Array2<f32>,
    linear_cache: LinearCache,
) -> (Array2<f32>, Array2<f32>, Array2<f32>) {
    let (a_prev, w, _b) = (linear_cache.a, linear_cache.w, linear_cache.b);
    let m = a_prev.shape()[1] as f32;
    let dw = (1.0 / m) * (dz.dot(&a_prev.reversed_axes()));
    let db_vec = ((1.0 / m) * dz.sum_axis(Axis(1))).to_vec();
    let db = Array2::from_shape_vec((db_vec.len(), 1), db_vec).unwrap();
    let da_prev = w.reversed_axes().dot(dz);

    (da_prev, dw, db)
}

The linear_backward function calculates the backward propagation for the linear component of a layer. It takes the gradient of the cost function with respect to the linear output dz and the linear cache linear_cache. It returns the gradients with respect to the previous layer’s activation da_prev, the weights dw, and the biases db.

The function first extracts the previous layer’s activation a_prev, the weight matrix w, and the bias matrix _b from the linear cache. It computes the number of training examples m by accessing the shape of a_prev and dividing the number of examples by m.

The function then calculates the gradient of the weights dw using the dot product between dz and the transposed a_prev, scaled by 1/m. It computes the gradient of the biases db by summing the elements of dz along Axis(1) and scaling the result by 1/m. Finally, it computes the gradient of the previous layer’s activation da_prev by performing the dot product between the transposed w and dz.

The function returns da_prev, dw, and db.

---

Backward Propagation

impl DeepNeuralNetwork {
    pub fn initialize_parameters(&self) -> HashMap<String, Array2<f32>> {
	// same as last part
    }
    pub fn forward(
        &self,
        x: &Array2<f32>,
        parameters: &HashMap<String, Array2<f32>>,
    ) -> (Array2<f32>, HashMap<String, (LinearCache, ActivationCache)>) {
    //same as last part
    }

	pub fn backward(
        &self,
        al: &Array2<f32>,
        y: &Array2<f32>,
        caches: HashMap<String, (LinearCache, ActivationCache)>,
    ) -> HashMap<String, Array2<f32>> {
        let mut grads = HashMap::new();
        let num_of_layers = self.layers.len() - 1;

        let dal = -(y / al - (1.0 - y) / (1.0 - al));

        let current_cache = caches[&num_of_layers.to_string()].clone();
        let (mut da_prev, mut dw, mut db) =
            linear_backward_activation(&dal, current_cache, "sigmoid");

        let weight_string = ["dW", &num_of_layers.to_string()].join("").to_string();
        let bias_string = ["db", &num_of_layers.to_string()].join("").to_string();
        let activation_string = ["dA", &num_of_layers.to_string()].join("").to_string();

        grads.insert(weight_string, dw);
        grads.insert(bias_string, db);
        grads.insert(activation_string, da_prev.clone());

        for l in (1..num_of_layers).rev() {
            let current_cache = caches[&l.to_string()].clone();
            (da_prev, dw, db) =
                linear_backward_activation(&da_prev, current_cache, "relu");

            let weight_string = ["dW", &l.to_string()].join("").to_string();
            let bias_string = ["db", &l.to_string()].join("").to_string();
            let activation_string = ["dA", &l.to_string()].join("").to_string();

            grads.insert(weight_string, dw);
            grads.insert(bias_string, db);
            grads.insert(activation_string, da_prev.clone());
        }

        grads
    }
	
    

The backward method in the DeepNeuralNetwork struct performs the backward propagation algorithm to calculate the gradients of the cost function with respect to the parameters (weights and biases) of each layer.

The method takes the final activation al obtained from the forward propagation, the true labels y, and the caches containing the linear and activation values for each layer.

First, it initializes an empty HashMap called grads to store the gradients. It computes the initial derivative of the cost function with respect to al using the provided formula.

Then, starting from the last layer (output layer), it retrieves the cache for the current layer and calls the linear_backward_activation function to calculate the gradients of the cost function with respect to the parameters of that layer. The activation function used is “sigmoid” for the last layer. The computed gradients for weights, biases, and activation are stored in the grads map.

Next, the method iterates over the remaining layers in reverse order. For each layer, it retrieves the cache, calls the linear_backward_activation function to calculate the gradients, and stores them in the grads map.

Finally, the method returns the grads map containing the gradients of the cost function with respect to each parameter of the neural network.

This completes the backward propagation step, where the gradients of the cost function are computed with respect to the weights, biases, and activations of each layer. These gradients will be used in the optimization step to update the parameters and minimize the cost.

---

Update Parameters

Let us now update the parameters using the gradients that we calculated.

    pub fn update_parameters(
        &self,
        params: &HashMap<String, Array2<f32>>,
        grads: HashMap<String, Array2<f32>>,
        m: f32, 
        learning_rate: f32,

    ) -> HashMap<String, Array2<f32>> {
        let mut parameters = params.clone();
        let num_of_layers = self.layer_dims.len() - 1;
        for l in 1..num_of_layers + 1 {
            let weight_string_grad = ["dW", &l.to_string()].join("").to_string();
            let bias_string_grad = ["db", &l.to_string()].join("").to_string();
            let weight_string = ["W", &l.to_string()].join("").to_string();
            let bias_string = ["b", &l.to_string()].join("").to_string();

            *parameters.get_mut(&weight_string).unwrap() = parameters[&weight_string].clone()
                - (learning_rate * (grads[&weight_string_grad].clone() + (self.lambda/m) *parameters[&weight_string].clone()) );
            *parameters.get_mut(&bias_string).unwrap() = parameters[&bias_string].clone()
                - (learning_rate * grads[&bias_string_grad].clone());
        }
        parameters
    }

In this code we go through each layer and update the parameters in the HashMap for each layer by using the HashMap of gradients in that layer. This will return us the updated parameters.

That’s all for this part. I know this was a little involved, but this is part is the heart of a deep neural network. Here are some resources that can help you understand the algorithm more visually.

An Overview of the Back Propagation Algorithm: https://www.youtube.com/watch?v=Ilg3gGewQ5U&t=203s

Calculus Behind the Back Propagation Algorithm: https://www.youtube.com/watch?v=tIeHLnjs5U8

In the next and final part of this series, we will run our training loop and test out our model on some cat 🐈 images

GitHub Repository: https://github.com/akshayballal95/dnn_rust_blog.git

---